Abstract
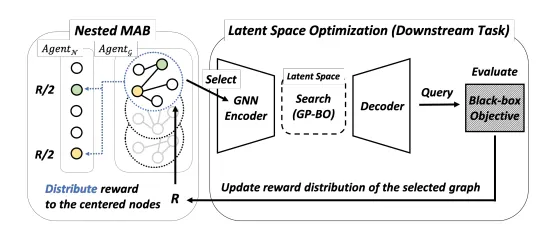
Real-world optimization problems are generally not just black-box problems, but also involve mixed types of inputs in which discrete and continuous variables coexist. Such mixed-space optimization possesses the primary challenge of modeling complex interactions between the inputs. In this work, we propose a novel yet simple approach that entails exploiting the graph data structure to model the underlying relationship between variables, i.e., variables as nodes and interactions defined by edges. Then, a variational graph autoencoder is used to naturally take the interactions into account. We first provide empirical evidence of the existence of such graph structures and then suggest a joint framework of graph structure learning and latent space optimization to adaptively search for optimal graph connectivity. Experimental results demonstrate that our method shows remarkable performance, exceeding the existing approaches with significant computational efficiency for a number of synthetic and real-world tasks.